单位圆 $D = \left\{ {(x , y)\mid {x^2} + {y^2} < 1} \right\}$ 内连接单位圆周 $C = \left\{ {(x , y)\mid {x^2} + {y^2} = 1} \right\}$ 上两个不同点且与 $C$ 在这两点处垂直的圆弧或直线段称为单位圆 $D$ 内的双曲直线（这里两条圆弧在交点处垂直是指这两条圆弧在交点处的切线垂直）．给定 $D$ 内一条双曲直线 $l$，则下列选项中正确的是 \((\qquad)\)
【难度】
【出处】
2010年复旦大学优秀高中生文化水平选拔测试
【标注】
【答案】
D
【解析】
我们将题目稍作改编，考虑更一般的情况：
若两条曲线 $f,g$ 在公共点 $P$ 处的切线互相垂直，那么称这两条曲线正交于点 $P$．
已知 $AB$ 是单位圆 $D$ 的一条弦，称与单位圆 $D$ 同时正交于点 $A$ 和点 $B$ 的圆弧 $AB$ 为 $D$ 的曲弦，记作 $(AB)$．当 $AB$ 是单位圆 $D$ 的直径时，定义曲弦 $(AB)$ 为直径 $AB$．
思考一：曲弦是个什么东西？
如图，
过圆外一点 $O'$ 引圆的两条切线 $O'P$ 和 $O'Q$，那么以 $O'$ 为圆心，切线长为半径作圆被单位圆所截的圆弧 $PQ$ 即为曲弦．
思考二：如何作过指定点的一条曲弦？
当指定点 $A$ 位于单位圆上时，作图是简单的，只需要作过 $A$ 的单位圆的切线，那么切线上任意一点 $O'$ 为圆心，$O'A$ 为半径作圆被单位圆所截得的圆弧即为过点 $A$ 的曲弦；
当指定点 $A$ 在单位圆内时，问题就复杂一些了．如图，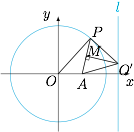
不妨设 $A(a,0)$，$P$ 为单位圆上任意一点，那么 $P$ 处单位圆的切线与线段 $AP$ 的垂直平分线的交点 $O'$ 即为过点 $A,P$ 的曲弦的圆心．利用解析几何知识可得 $O'$ 的轨迹是直线 $x=\dfrac 12\left(a+\dfrac 1a\right)$．
这就意味着，只要作出单位圆内一点 $A$ 对应的直线 $l(A)$，在 $l(A)$ 上任取一点 $O'$ 作为圆心，$O'A$ 为半径作圆被单位圆所截得的圆弧即为过点 $A$ 的曲弦．
思考三：如何作过指定两点的一条曲弦？
继续前面的思考．
当指定两点 $A,B$ 与圆心 $O$ 不共线时，作直线 $l(A)$ 和 $l(B)$，取其交点为曲弦圆心即可；当指定两点 $A,B$ 与圆心 $O$ 共线（包含其中一点为 $O$ 的情形）时，过 $A,B$ 的直径即为所求曲弦．
接下来，我们来看看选项．
对于选项A，取直径 $AB$，从点 $A$ 出发作一系列与 $AB$ 垂直的曲弦，最后汇聚到 $B$，如图，
这些曲弦会经过圆内的任何一点，因此命题成立；
对于选项B，如果两条曲弦相切于圆内一点 $A$，那么它们的圆心必然同在直线 $l(A)$ 上，此时 $A\notin l(A)$，因此与两条曲弦相切矛盾，因此命题成立；
对于选项C，根据思考三，命题错误；
对于选项D，与对选项A的思考类似，对任意曲弦 $(AB)$，我们都可以作一系列曲弦 $(CD)$（保持 $CD\parallel AB$），而这一系列曲弦 $(CD)$ 将扫过整个单位圆及其内部，因此命题成立．
因此正确答案是C．
若两条曲线 $f,g$ 在公共点 $P$ 处的切线互相垂直，那么称这两条曲线正交于点 $P$．
已知 $AB$ 是单位圆 $D$ 的一条弦，称与单位圆 $D$ 同时正交于点 $A$ 和点 $B$ 的圆弧 $AB$ 为 $D$ 的曲弦，记作 $(AB)$．当 $AB$ 是单位圆 $D$ 的直径时，定义曲弦 $(AB)$ 为直径 $AB$．
思考一：曲弦是个什么东西？
如图，
过圆外一点 $O'$ 引圆的两条切线 $O'P$ 和 $O'Q$，那么以 $O'$ 为圆心，切线长为半径作圆被单位圆所截的圆弧 $PQ$ 即为曲弦．思考二：如何作过指定点的一条曲弦？
当指定点 $A$ 位于单位圆上时，作图是简单的，只需要作过 $A$ 的单位圆的切线，那么切线上任意一点 $O'$ 为圆心，$O'A$ 为半径作圆被单位圆所截得的圆弧即为过点 $A$ 的曲弦；
当指定点 $A$ 在单位圆内时，问题就复杂一些了．如图，
不妨设 $A(a,0)$，$P$ 为单位圆上任意一点，那么 $P$ 处单位圆的切线与线段 $AP$ 的垂直平分线的交点 $O'$ 即为过点 $A,P$ 的曲弦的圆心．利用解析几何知识可得 $O'$ 的轨迹是直线 $x=\dfrac 12\left(a+\dfrac 1a\right)$．这就意味着，只要作出单位圆内一点 $A$ 对应的直线 $l(A)$，在 $l(A)$ 上任取一点 $O'$ 作为圆心，$O'A$ 为半径作圆被单位圆所截得的圆弧即为过点 $A$ 的曲弦．
思考三：如何作过指定两点的一条曲弦？
继续前面的思考．
当指定两点 $A,B$ 与圆心 $O$ 不共线时，作直线 $l(A)$ 和 $l(B)$，取其交点为曲弦圆心即可；当指定两点 $A,B$ 与圆心 $O$ 共线（包含其中一点为 $O$ 的情形）时，过 $A,B$ 的直径即为所求曲弦．
接下来，我们来看看选项．
对于选项A，取直径 $AB$，从点 $A$ 出发作一系列与 $AB$ 垂直的曲弦，最后汇聚到 $B$，如图，
这些曲弦会经过圆内的任何一点，因此命题成立；对于选项B，如果两条曲弦相切于圆内一点 $A$，那么它们的圆心必然同在直线 $l(A)$ 上，此时 $A\notin l(A)$，因此与两条曲弦相切矛盾，因此命题成立；
对于选项C，根据思考三，命题错误；
对于选项D，与对选项A的思考类似，对任意曲弦 $(AB)$，我们都可以作一系列曲弦 $(CD)$（保持 $CD\parallel AB$），而这一系列曲弦 $(CD)$ 将扫过整个单位圆及其内部，因此命题成立．
因此正确答案是C．
题目
答案
解析
备注
