设 ${F_1},{F_2}$ 分别为椭圆 $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1$ 的左、右焦点,且点 $P$ 是椭圆上的一点.若 ${F_1},{F_2},P$ 是一个直角三角形的三个顶点,则点 $P$ 到 $x$ 轴的距离为 \((\qquad)\)
【难度】
【出处】
2008年复旦大学优秀高中生文化水平选拔测试
【标注】
【答案】
B
【解析】
如图,有两种可能.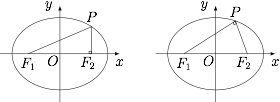
情形一 若 $P$ 不为直角顶点,则 $P$ 到 $x$ 轴的距离为半通径长,为$$\dfrac{{{b^2}}}{a} = \dfrac{9}{4};$$情形二 若 $P$ 为直角顶点,则 $P$ 点坐标满足$$\begin{cases} \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{9} = 1 ,\\ {x^2} + {y^2} = 7 ,\\\end{cases}$$解得 ${y^2} = \dfrac{{81}}{7} > 9 $,舍去.
综上,$ \dfrac{9}{4}$ 为所求.

综上,$ \dfrac{9}{4}$ 为所求.
题目
答案
解析
备注