以立方体中三条两两异面的棱为例，配示意图如下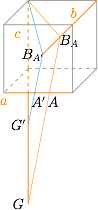：在直线 $a$ 上任取点 $A$，设点 $A$ 与直线 $c$ 确定的平面为 $\alpha_A$，那么这样的平面有无数个，且这些平面都交于直线 $c$．
与直线 $b$ 相交的平面 $\alpha(A)$ 有无数个，这是因为直线 $b$ 至多和这些平面中的一个平行，否则假设 $b$ 与 $\alpha_{A}$ 和 $\alpha_{A'}$ 均平行，那么 $b$ 和 $A,A'$ 所确定的平面与 $\alpha_{A},\alpha_{A'}$ 的交线 $l_1,l_2$ 均与 $b$ 平行．
考虑 $l_1,l_2$ 形成的平面与平面 $\alpha_{A},\alpha_{A'}$，根据透视原理，它们两两的交线两两平行，于是 $b\parallel c$，矛盾．
设直线 $b$ 与平面 $\alpha_A$ 相交于点 $B_A$，考虑直线 $AB_A$，当 $A$ 变化时一系列直线 $AB_A$ 中至多只有一条与 $c$ 平行，否则 $AB_{A}\parallel A'B_{A'}\parallel c$，于是 $A,B_{A},A',B_{A'}$ 四点共面，进而 $a,b$ 共面，矛盾．这样就构造出了无数条符合题意的直线 $AB_A$．