欲将正六边形的各边和各条对角线都染为 $n$ 种颜色之一，使得以正六边形的任何 $3$ 个顶点作为顶点的三角形有 $3$ 种不同颜色的边，并且不同的三角形使用不同的 $3$ 色组合，则 $n$ 的最小值为 \((\qquad)\)
【难度】
【出处】
2010年清华大学等五校合作自主选拔通用基础测试数学试题
【标注】
【答案】
B
【解析】
因为正六边形的顶点所形成的三角形共 $\mathrm{C}_6^3$ 个，所以 $n$ 种颜色的 $3$ 色组合至少要有 $\mathrm{C}_6^3$ 种，即$$n\geqslant6.$$情形一 $n=6$，因为 $6$ 种颜色的 $3$ 色组合有 $\mathrm{C}_6^3$ 种，而且由已知这些三角形的 $3$ 色组合都不同，所以 $6$ 种颜色所有的 $3$ 色组合都恰好出现一次．
另一方面，$6$ 个顶点的连线共 $\mathrm{C}_6^2 = 15$ 条，因此存在一种颜色只有 $2$ 条，含有这种颜色的三角形只有 $2 \times 4 = 8$ 个，但含有此种颜色的 $3$ 色组合却有 $\mathrm{C}_5^2 = 10$ 种，这与 $3$ 色组合都出现一次矛盾，故 $6$ 种颜色不行．
情形二 $n=7$，如图，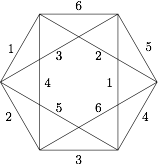
图中数字分别对应某种颜色，共使用了 $6$ 种颜色，剩下的 $3$ 条对角线染第 $7$ 种颜色，则满足要求．
另一方面，$6$ 个顶点的连线共 $\mathrm{C}_6^2 = 15$ 条，因此存在一种颜色只有 $2$ 条，含有这种颜色的三角形只有 $2 \times 4 = 8$ 个，但含有此种颜色的 $3$ 色组合却有 $\mathrm{C}_5^2 = 10$ 种，这与 $3$ 色组合都出现一次矛盾，故 $6$ 种颜色不行．
图中数字分别对应某种颜色，共使用了 $6$ 种颜色，剩下的 $3$ 条对角线染第 $7$ 种颜色，则满足要求．
题目
答案
解析
备注
