查看数据源：59128839e020e7000878f8fa
在正三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，若 $B{B_1} = \dfrac{{\sqrt 2 }}{2}AB$，则 ${C_1}B$ 与 $A{B_1}$ 所成角的大小为 \((\qquad)\)
A: $15^\circ$
B: $75^\circ$
C: $90^\circ $
D: $60^\circ $
【难度】
【出处】
2008年西北工业大学自主招生测试
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    异面直线所成的角
【答案】
C
【解析】
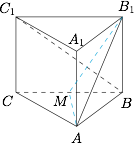
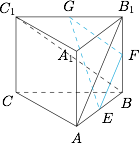解法一取 $BC$ 的中点 $M$，连结 $AM,B_1M$，则有 $B_1M\perp BC_1$，从而 $AB_1\perp BC_1$．解法二取 $AB$，$BB_1$，$B_1C_1$ 中点 $E$，$F$，$G$，则 $C_1B$ 与 $AB_1$ 所成的角等于 $\angle EFG$．容易计算得到 $EF$，$EG$，$FG$ 的长度，且$$ |EG|^2=|EF|^2+|FG|^2,$$所以 $C_1B$ 与 $AB_1$ 所成的角大小为 $90^\circ$．
题目 答案 解析 备注
0.109619s