查看数据源：591288ace020e7000a798b91
如果直线 $y = kx + 1$ 与圆 ${x^2} + {y^2} + kx + my - 4 = 0$ 交于 $M,N$ 两点，且 $M,N$ 关于直线 $x - y = 0$ 对称，动点 $P\left( {a, b} \right)$ 在不等式组 $\begin{cases}kx - y + 2 \geqslant 0,\\kx - my \leqslant 0,\\y \geqslant 0\end{cases}$，表示的平面区域的内部及边界上运动，则点 $A\left( {1, 2} \right)$ 与点 $P$ 连线的斜率的取值范围是 \((\qquad)\)
A: $\left[ {2, + \infty } \right)$
B: $\left( { - \infty , - 2} \right]$
C: $\left[ { - 2, 2} \right]$
D: $\left( { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right)$
【难度】
【出处】
2008年西北工业大学自主招生测试
【标注】
  • 方法
    >
    数形结合
    >
    不等式(组)的规划
  • 知识点
    >
    解析几何
    >
    圆
    >
    圆的方程
    >
    圆的标准方程
【答案】
D
【解析】
由 $M,N$ 关于直线 $x-y=0$ 对称，可得 $k=-1$，而圆心在 $y = x$ 上，所以$$m=k=-1.$$可行域如图阴影所示，斜率在 $AO,AB$ 取得临界值．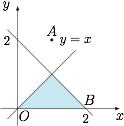
题目 答案 解析 备注
0.121126s