查看数据源：5964972322a5da0007aed4be
如图是某几何体的三视图，其中正视图为正方形，俯视图是腰长为 $2$ 的等腰直角三角形，则该几何体的体积是  \((\qquad)\)
A: $\dfrac {8}{3}$
B: $\dfrac {8\sqrt 2}{3}$
C: $\dfrac {4}{3}$
D: $\dfrac {4\sqrt 2}{3}$
【难度】
【出处】
2014年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
D
【解析】
由三视图可知，该几何体是将一个棱长为 $2$ 的正方体沿某个面的对角线截去一半后，又截去一个完整的角所得到的四棱锥，如图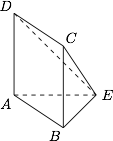．因此该几何体的体积为$$\dfrac 13\cdot 4\cdot \sqrt 2=\dfrac {4\sqrt 2}{3}.$$
题目 答案 解析 备注
0.110456s