一群学生参加学科夏令营，每名同学至少参加一个学科考试．已知有 $100$ 名学生参加了数学考试，$50$ 名学生参加了物理考试，$48$ 名学生参加了化学考试．学生总数是参加至少两门考试学生数的两倍，也是参加三门考试学生数的三倍，则学生总数为 \((\qquad)\)
【难度】
【出处】
2017年北京大学博雅计划数学试题
【标注】
【答案】
A
【解析】
设只参加了数学、物理、化学考试的学生数分别为 $x,y,z$；参加了两门学科考试的同学中参加了数学和物理、物理和化学、化学和数学的学生数分别为 $c,a,b$；同时参加了三门学科考试的学生数为 $m$，如图．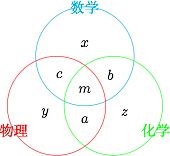
根据题意，有\[\begin{cases}x+b+c+m=100,\\ y+c+a+m=50,\\ z+a+b+m=48,\\
x+y+z+a+b+c+m=2(x+y+z)=3m,\end{cases}\]前面三个等式相加，可得\[x+y+z+2(a+b+c)+3m=198.\]由第四个等式可得\begin{align*}x+y+z&=\dfrac 32m,\\
a+b+c&=\dfrac m2,
\end{align*}代入可得\[\dfrac 32m+m+3m=198,\]解得 $m=36$．因此学生总数为 $3m=108$．
根据题意，有\[\begin{cases}x+b+c+m=100,\\ y+c+a+m=50,\\ z+a+b+m=48,\\x+y+z+a+b+c+m=2(x+y+z)=3m,\end{cases}\]前面三个等式相加，可得\[x+y+z+2(a+b+c)+3m=198.\]由第四个等式可得\begin{align*}x+y+z&=\dfrac 32m,\\
a+b+c&=\dfrac m2,
\end{align*}代入可得\[\dfrac 32m+m+3m=198,\]解得 $m=36$．因此学生总数为 $3m=108$．
题目
答案
解析
备注
