在平面直角坐标系中，$\triangle ABC$ 的顶点坐标分别为 $A\left({3,4}\right)$，$B\left({6,0}\right)$，$C\left({-5,-2}\right)$，则 $\angle A$ 的平分线所在直线的方程为 \((\qquad)\)
【难度】
【出处】
2006年复旦大学自主选拔录取申请资格测试（B卷）
【标注】
【答案】
A
【解析】
如图，其中 $AD$ 为 $\angle A$ 的平分线．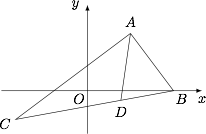
由于 $AB=5$，$AC=10$，于是\[\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac 12,\]从而由定比分点坐标公式，可得 $D\left(\dfrac 73,-\dfrac 23\right)$，于是直线 $AD$ 的斜率为\[\dfrac{4-\left(-\dfrac 23\right)}{3-\dfrac 73}=7.\]
由于 $AB=5$，$AC=10$，于是\[\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac 12,\]从而由定比分点坐标公式，可得 $D\left(\dfrac 73,-\dfrac 23\right)$，于是直线 $AD$ 的斜率为\[\dfrac{4-\left(-\dfrac 23\right)}{3-\dfrac 73}=7.\]
题目
答案
解析
备注
