在矩形 $ABCD$ 中,$AB=1$,$AD=2$,动点 $P$ 在以点 $C$ 为圆心且与 $BD$ 相切的圆上,若 $\overrightarrow{AP}=\lambda \overrightarrow{AB}+\mu \overrightarrow{AD}$,则 $\lambda+\mu$ 的最大值为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
如图,考虑向量线性分解的等系数和线,可得 $\lambda+\mu$ 的最大值为 $3$.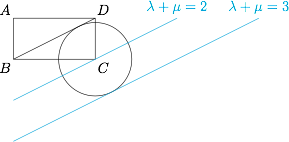
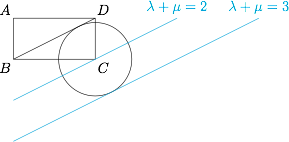
题目
答案
解析
备注