半径为 $R$ 的球内部装有 $4$ 个有相同半径的小球，则小球半径 $r$ 的可能的最大值为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
B
【解析】
如图，四个球的球心组成棱长为 $2r$ 的正四面体，所以 $OA = \dfrac{{\sqrt 6 }}{2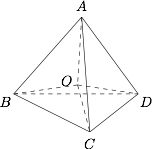}r$．
又因为$$OA = OB = OC = OD = R - r,$$因此 $r = \dfrac{{\sqrt 6 }}{{3 + \sqrt 6 }}R$．
又因为$$OA = OB = OC = OD = R - r,$$因此 $r = \dfrac{{\sqrt 6 }}{{3 + \sqrt 6 }}R$．
题目
答案
解析
备注
