查看数据源：5968835722d140000ac07f02
记 $[x]$ 为不超过 $x$ 的最大整数．若集合 $S=\big\{(x,y)\mid \big|[x+y]\big|+\big|[x-y]\big|\leqslant 1\big\}$，则集合 $S$ 所表示的平面区域的面积为 \((\qquad)\)
A: $\dfrac{5}{2}$
B: $3$
C: $\dfrac{9}{2}$
D: $4$
【难度】
【出处】
2016年全国高中数学联赛浙江省预赛
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    高斯函数
  • 方法
    >
    数形结合
    >
    不等式(组)的规划
【答案】
A
【解析】
情形一 当 $0\leqslant x+y<1$ 时，$[x+y]=0$，所以$$\big|[x-y]\big|\leqslant 1,$$即 $-1\leqslant x-y<2$．
情形二 当 $1\leqslant x+y<2$ 时，$[x+y]=1$，所以$$\big|[x-y]\big|=0,$$即 $0\leqslant x-y<1$．
情形三 当 $-1\leqslant x+y<0$ 时，$[x+y]=-1$，所以$$\big|[x-y]\big|=0,$$即 $0\leqslant x-y<1$．
画出满足上述条件的区域，可知集合 $S$ 所表示的平面区域的面积为 $\dfrac{5}{2}$．
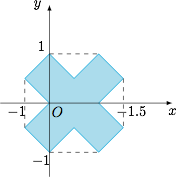
题目 答案 解析 备注
0.109150s