$O$ 是正三棱锥 $P-ABC$ 底面三角形 $ABC$ 的中心,过点 $O$ 的动平面与 $PC$ 交于 $S$,与射线 $PA,PB$ 分别交于 $Q,R$,则 $\dfrac{1}{PQ}+\dfrac{1}{PR}+\dfrac{1}{PS}$ \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
如图,设 $\angle APB=\angle BPC=\angle CPA=\theta$,$PQ=a,PR=b,PS=c$,$O$ 到平面 $PAB,PBC,PCA$ 的距离相等,设为 $d$,则 $PC$ 与平面 $PAB$ 所成的角 $\alpha$,满足 $\cos\alpha=\cos\dfrac{\theta}{2}\cdot\cos\theta$,因此$$V_{S-PQR}=V_{O-PQR}+V_{O-PRS}+V_{O-PQS},$$整理得$$\dfrac1a+\dfrac1b+\dfrac1c=\dfrac{\sin\alpha}{d},$$而 $\sin\alpha$ 及 $d$ 均为与面 $QPS$ 无关的常数.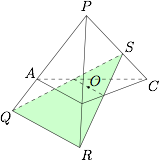

题目
答案
解析
备注