已知三棱锥 $S-ABC$ 的所有顶点都在球 $O$ 的球面上，$\triangle ABC$ 是边长为 $1$ 的正三角形，$SC$ 为球 $O$ 的直径，且 $SC=2$，则此棱锥的体积为 \((\qquad)\)
【难度】
【出处】
2012年高考新课标全国卷（理）
【标注】
【答案】
A
【解析】
如图．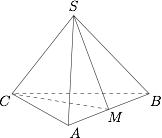
有$$\cos\angle SCM=\dfrac{\cos\angle SCA}{\cos\angle MCA}=\dfrac{1}{\sqrt3},$$所以$$\sin\angle SCM=\dfrac{\sqrt2}{\sqrt3},$$于是$$V_{S-ABC}=\dfrac13\cdot S_{\triangle SCM}\cdot AB=\dfrac{\sqrt2}{6}.$$
有$$\cos\angle SCM=\dfrac{\cos\angle SCA}{\cos\angle MCA}=\dfrac{1}{\sqrt3},$$所以$$\sin\angle SCM=\dfrac{\sqrt2}{\sqrt3},$$于是$$V_{S-ABC}=\dfrac13\cdot S_{\triangle SCM}\cdot AB=\dfrac{\sqrt2}{6}.$$
题目
答案
解析
备注
