某几何体的一条棱长为 $\sqrt7$，在该几何体的正视图中，这条棱的投影是长为 $\sqrt6$ 的线段，在该几何体的侧视图和俯视图中，这条棱的投影分别是长为 $a$ 和 $b$ 的线段，则 $a+b$ 的最大值为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
如图，以 $AC_1=\sqrt{7}$ 为体对角线构造长方体 $ABCD-A_1B_1C_1D_1$．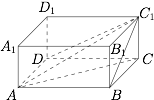
长方体 $AC_1$ 的正视图，俯视图，侧视图中的投影分别为 $DC_1,BC_1,AC$，所以$$a^2+b^2+(\sqrt6)^2=14,$$解得 $a^2+b^2=8$，设 $a=2\sqrt2\cos\theta,b=2\sqrt2\sin\theta$，所以$$a+b=4\sin\left(\alpha+\dfrac{\pi}{4}\right),$$因此 $a+b$ 的最大值为 $4$．
长方体 $AC_1$ 的正视图，俯视图，侧视图中的投影分别为 $DC_1,BC_1,AC$，所以$$a^2+b^2+(\sqrt6)^2=14,$$解得 $a^2+b^2=8$，设 $a=2\sqrt2\cos\theta,b=2\sqrt2\sin\theta$，所以$$a+b=4\sin\left(\alpha+\dfrac{\pi}{4}\right),$$因此 $a+b$ 的最大值为 $4$．
题目
答案
解析
备注
