查看数据源：597fcc11d05b90000c805a2c
已知 $ABCD-A_1B_1C_1D_1$ 为正方体，任取平面 $\alpha$ 与对角线 $AC_1$ 垂直，使得 $\alpha$ 与正方体的每个面都有公共点，记这样得到的截面多边形的面积为 $S$，周长为 $l$，则 \((\qquad)\)
A: $S$ 为定值，$l$ 不为定值
B: $S$ 不为定值，$l$ 为定值
C: $S,l$ 均为定值
D: $S,l$ 均不为定值
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的截面
【答案】
B
【解析】
如图，显然 $S$ 不为定值，$l$ 为定值．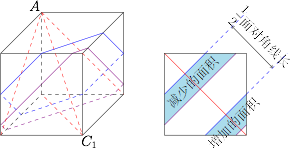
题目 答案 解析 备注
0.158444s