设函数 $f(x)=\dfrac{a^2+a\sin x+2}{a^2+a\cos x+2}$($x\in \mathbb R$)的最大值为 $M(a)$,最小值为 $m(a)$,则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
当 $a=0$ 时,$M(a)=m(a)=1$;
当 $a\ne 0$ 时,有$$f(x)=\dfrac{\sin x-\left[-\left(a+\dfrac 2a\right)\right]}{\cos x -\left[-\left(a+\dfrac 2a\right)\right]},$$设点 $A\left(\cos x,\sin x\right)$,$B\left(-\left(a+\dfrac 2a\right),-\left(a+\dfrac 2a\right)\right)$,则 $f(x)$ 的几何意义即直线 $AB$ 的斜率.点 $A$ 为单位圆上的动点,点 $B$ 为两条射线上的定点,根据图形的对称性可得 $M(a)\cdot m(a)=1$.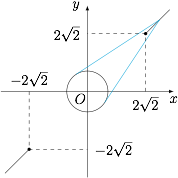
当 $a\ne 0$ 时,有$$f(x)=\dfrac{\sin x-\left[-\left(a+\dfrac 2a\right)\right]}{\cos x -\left[-\left(a+\dfrac 2a\right)\right]},$$设点 $A\left(\cos x,\sin x\right)$,$B\left(-\left(a+\dfrac 2a\right),-\left(a+\dfrac 2a\right)\right)$,则 $f(x)$ 的几何意义即直线 $AB$ 的斜率.点 $A$ 为单位圆上的动点,点 $B$ 为两条射线上的定点,根据图形的对称性可得 $M(a)\cdot m(a)=1$.

题目
答案
解析
备注