查看数据源：59e851c3c3f07000082a37f6
如图所示，已知圆锥的底面半径为 $7$，母线长为 $14$，$FC$ 是轴截面 $ABC$ 底角 $\angle{ACB}$ 的平分线，$BD$ 是底面的一条弦，且 $\angle{DBC}=30^{\circ}$，则直线 $FC$ 与 $BD$ 的距离是 \((\qquad)\)
A: $\sqrt{14}$
B: $2\sqrt 7$
C: $3\sqrt 7$
D: $\dfrac 72$
【难度】
【出处】
2012年第二十三届“希望杯”全国数学邀请赛高一（二试）
【标注】
  • 数学竞赛
    >
    立体几何
    >
    空间计算
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的距离
    >
    异面直线间的距离
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    利用向量计算空间几何量
【答案】
B
【解析】
由题可知 $BD\perp DC$，以 $D$ 为坐标原点，建立空间直角坐标系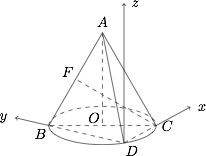，计算可得$$\overrightarrow{CF}=\left(-\dfrac{21}{4},\dfrac{21\sqrt 3}{4},\dfrac{7\sqrt 3}{2}\right),\overrightarrow{DB}=\left(0,7\sqrt 3,0\right).$$设 $\overrightarrow{n}=(x,y,z)$，且 $\overrightarrow{n}\perp \overrightarrow{CF}$，$\overrightarrow{n}\perp \overrightarrow{DB}$，可求得$$\overrightarrow{n}=\left(2,0,\sqrt 3\right).$$设 $d$ 为直线 $FC$ 与 $BD$ 间的距离，则$$d=\dfrac{\left|\overrightarrow{BF}\cdot \overrightarrow{n}\right|}{\left|\overrightarrow{n}\right|}=2\sqrt 7.$$
题目 答案 解析 备注
0.108942s