在平面中，到两条相交直线的距离之和为 $1$ 的点的轨迹为 \((\qquad)\)
【难度】
【出处】
2008年全国高中数学联赛安徽省预赛
【标注】
【答案】
D
【解析】
先考虑一种特殊情况：两直线互相垂直时．
以交点为坐标原点，以两直线分别为 $x$ 轴，$y$ 轴，建立直角坐标系．
由题意知，满足条件的点的坐标满足的方程为$$|x|+|y|=1,$$显然该点的轨迹组成了一个矩形．
下面只需证明任意矩形各边上的点到两对角线的距离之和为定值．
如图，$E,F$ 是矩形 $ABCD$ 边上的任意两点，$E_1,E_2,F_1,F_2$ 为这两点向对角线做垂线的垂足．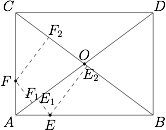
设 $\angle BAD=\alpha$，则$$\begin{split}&FF_1+FF_2=AC\cdot \cos \alpha,\\&EE_1+EE_2=AB\sin \alpha.\end{split}$$又因为$$\tan \alpha =\dfrac {BD}{AB},$$所以$$FF_1+FF_2=EE_1+EE_2.$$因此，题设条件下的点的轨迹为一个矩形．
以交点为坐标原点，以两直线分别为 $x$ 轴，$y$ 轴，建立直角坐标系．
由题意知，满足条件的点的坐标满足的方程为$$|x|+|y|=1,$$显然该点的轨迹组成了一个矩形．
下面只需证明任意矩形各边上的点到两对角线的距离之和为定值．
如图，$E,F$ 是矩形 $ABCD$ 边上的任意两点，$E_1,E_2,F_1,F_2$ 为这两点向对角线做垂线的垂足．
设 $\angle BAD=\alpha$，则$$\begin{split}&FF_1+FF_2=AC\cdot \cos \alpha,\\&EE_1+EE_2=AB\sin \alpha.\end{split}$$又因为$$\tan \alpha =\dfrac {BD}{AB},$$所以$$FF_1+FF_2=EE_1+EE_2.$$因此，题设条件下的点的轨迹为一个矩形．
题目
答案
解析
备注
