查看数据源：59f15c2c9552360008e02f5d
有长为 $\sqrt 2$ 宽为 $1$ 的矩形，以它的一条对角线所在的直线为轴将其在轴线一侧的部分旋转一周，则所得到的旋转体的体积为 \((\qquad)\)
A: $\dfrac{3\sqrt 3}{8}\pi$
B: $\dfrac{2\sqrt 3}{9}\pi$
C: $\dfrac{29\sqrt 3}{72}\pi$
D: $\dfrac{23\sqrt 3}{72}\pi$
【难度】
【出处】
2011年第二十二届“希望杯”全国数学邀请赛高一（二试）
【标注】
  • 数学竞赛
    >
    立体几何
    >
    空间几何体
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
【答案】
B
【解析】
如图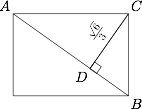．根据题意，以 $AB$ 为旋转轴旋转所得到旋转体的体积 $V$ 即为直角三角形 $ABC$ 绕 $AB$ 旋转后所得旋转体的体积，故$$V= \dfrac{1}{3}\cdot \pi\cdot \left(\dfrac{\sqrt 6}{3}\right)^2\cdot \sqrt 3=\dfrac{2\sqrt 3}{9}\pi.$$
题目 答案 解析 备注
0.108996s