圆 $O:x^2+y^2=r^2$（$r>0$）与 $x$ 轴正半轴交于点 $A$，且与直线 $l:y=kx+2$ 交于点 $B$ 和 $C$（$B$ 在 $x$ 轴上方），若 $\angle{ABC}=60^{\circ}$，$AC=4$，则原点 $O$ 到 $l$ 的距离是 \((\qquad)\)
【难度】
【出处】
2011年第二十二届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
D
【解析】
如图．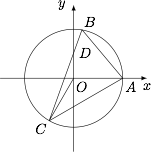
根据题意，$\angle{ABC}=60^{\circ}$，可得 $\angle{AOC}=120^{\circ}$，所以 $\angle{COD}=150^{\circ}$．
因为 $AC=4$，故由正弦定理可得$$2r=\dfrac 4{\sin{60^{\circ}}},$$解得$$r=\dfrac{4}{\sqrt 3}.$$在 $\triangle{ODC}$ 中，$OD=2$．由余弦定理可得$$CD=\dfrac{2\sqrt{39}}{3}.$$设 $O$ 到 $l$ 的距离为 $d$，则$$\dfrac 12 \cdot OC\cdot OD\cdot \sin{150^{\circ}}=\dfrac 12 \cdot CD\cdot d,$$解得$$d=\dfrac{2\sqrt{13}}{13}.$$
根据题意，$\angle{ABC}=60^{\circ}$，可得 $\angle{AOC}=120^{\circ}$，所以 $\angle{COD}=150^{\circ}$．因为 $AC=4$，故由正弦定理可得$$2r=\dfrac 4{\sin{60^{\circ}}},$$解得$$r=\dfrac{4}{\sqrt 3}.$$在 $\triangle{ODC}$ 中，$OD=2$．由余弦定理可得$$CD=\dfrac{2\sqrt{39}}{3}.$$设 $O$ 到 $l$ 的距离为 $d$，则$$\dfrac 12 \cdot OC\cdot OD\cdot \sin{150^{\circ}}=\dfrac 12 \cdot CD\cdot d,$$解得$$d=\dfrac{2\sqrt{13}}{13}.$$
题目
答案
解析
备注
