如图，已知 $\triangle ABC$ 的顶点坐标分别为 $A(0,2),B(1,0),C(2,1)$，若二次函数 $y=x^2+bx+1$ 的图象与阴影部分（含边界）一定有公共点，则实数 $b$ 的取值范围是 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
二次函数 $y=x^2+bx+1=\left(x+\dfrac b2\right)^2+1-\dfrac{b^2}4$．
如图．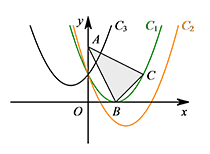
当抛物线 $C_1$ 经过点 $B(1,0)$，即 $b=-2$ 时，
此时点 $B$ 为抛物线的顶点，点 $C$ 也在抛物线上；
当抛物线 $C_2$ 的对称轴在直线 $x=1$ 的右侧，即 $b<-2$ 时，
此时抛物线与阴影部分（含边界）无公共点；
当抛物线 $C_3$ 的对称轴在直线 $x=1$ 的左侧，即 $b>-2$ 时，
此时抛物线与阴影部分（含边界）始终有公共点．
综上可得，实数 $b$ 的取值范围是 $b\geqslant -2$．
如图．
当抛物线 $C_1$ 经过点 $B(1,0)$，即 $b=-2$ 时，此时点 $B$ 为抛物线的顶点，点 $C$ 也在抛物线上；
当抛物线 $C_2$ 的对称轴在直线 $x=1$ 的右侧，即 $b<-2$ 时，
此时抛物线与阴影部分（含边界）无公共点；
当抛物线 $C_3$ 的对称轴在直线 $x=1$ 的左侧，即 $b>-2$ 时，
此时抛物线与阴影部分（含边界）始终有公共点．
综上可得，实数 $b$ 的取值范围是 $b\geqslant -2$．
题目
答案
解析
备注
