已知存在实数 $r$,使得圆周 $x^2+y^2=r^2$ 上恰好有 $n$ 个整点,则 $n$ 可以等于 \((\qquad)\)
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
【答案】
ACD
【解析】
由对称性可知 $n$ 必然为 $4$ 的倍数,当 $r=1,\sqrt 5,5$ 时,$n$ 分别为 $4,8,12$,如图.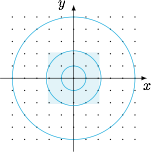

题目
答案
解析
备注