设 $E,F,G$ 分别是正四面体 $ABCD$ 的棱 $AB,BC,CD$ 的中点,则二面角 $C-FG-E$ 的大小是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
不妨设正四面体的棱长为 $2$.
如图,设 $H$ 为 $E$ 在底面上的投影,则在 $\triangle EFG$ 中,$$EF=GF=1,EG=\sqrt2,$$所以 $S_{\triangle EFG}=\dfrac12$.
在 $\triangle GFH$ 中,$$GF=1,FH=\dfrac{\sqrt3}{3},$$所以 $S_{\triangle GFH}=\dfrac{\sqrt3}{6}$.
设二面角 $E-FG-H$ 的大小为 $\theta$,则$$\cos\theta=\dfrac{1}{\sqrt3},\sin\theta=\dfrac{\sqrt2}{\sqrt3},\tan\theta=\sqrt2,$$所以$$\theta=\pi-\arcsin\dfrac{\sqrt6}{3}=\pi-\arccos\dfrac{\sqrt3}{3}=\pi-\arctan\sqrt2.$$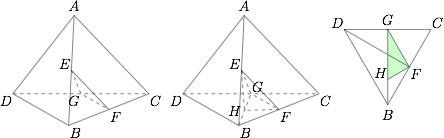
如图,设 $H$ 为 $E$ 在底面上的投影,则在 $\triangle EFG$ 中,$$EF=GF=1,EG=\sqrt2,$$所以 $S_{\triangle EFG}=\dfrac12$.
在 $\triangle GFH$ 中,$$GF=1,FH=\dfrac{\sqrt3}{3},$$所以 $S_{\triangle GFH}=\dfrac{\sqrt3}{6}$.
设二面角 $E-FG-H$ 的大小为 $\theta$,则$$\cos\theta=\dfrac{1}{\sqrt3},\sin\theta=\dfrac{\sqrt2}{\sqrt3},\tan\theta=\sqrt2,$$所以$$\theta=\pi-\arcsin\dfrac{\sqrt6}{3}=\pi-\arccos\dfrac{\sqrt3}{3}=\pi-\arctan\sqrt2.$$

题目
答案
解析
备注