直线 $l$ 经过椭圆的一个顶点和一个焦点，若椭圆中心到 $l$ 的距离为其短轴长的 $\dfrac 14$，则该椭圆的离心率为 \((\qquad)\)
【难度】
【出处】
2016年高考全国乙卷（文）
【标注】
【答案】
B
【解析】
如图所示，$l$ 经过椭圆的左焦点 $F$ 和上顶点 $B$，$OA\perp l$，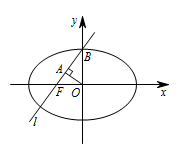
设\[|OF|=c,|OB|=b,\]则\[|OA|=\dfrac 14\times 2b=\dfrac 12b.\]在 $\mathrm{Rt}\triangle OFB$ 中\[|OF|\times|OB|=|BF|\times|OA|,\]代入上式结合 $a^2=b^2+c^2$ 可解得\[a=2c.\]所以椭圆的离心率为 $\dfrac 12$．故选B．
设\[|OF|=c,|OB|=b,\]则\[|OA|=\dfrac 14\times 2b=\dfrac 12b.\]在 $\mathrm{Rt}\triangle OFB$ 中\[|OF|\times|OB|=|BF|\times|OA|,\]代入上式结合 $a^2=b^2+c^2$ 可解得\[a=2c.\]所以椭圆的离心率为 $\dfrac 12$．故选B．
题目
答案
解析
备注
