记椭圆 $\dfrac{x^2}{4} + \dfrac{{n{y^2}}}{4n + 1} = 1$ 围成的区域（含边界）为 ${\Omega _n}\left( {n = 1,2, \cdots } \right)$，当点 $\left( {x,y} \right)$ 分别在 ${\Omega _1}$，${\Omega _2}$，$ \cdots $ 上时，$x + y$ 的最大值分别是 ${M_1}$，${M_2}$，$ \cdots $，则 $ \lim \limits_{n \to \infty } {M_n} = $ \((\qquad)\)
【难度】
【出处】
2013年高考上海卷（文）
【标注】
【答案】
D
【解析】
椭圆方程可变形为 $\dfrac {x^2}4+\dfrac {y^2}{4+\dfrac 1n}=1$，当 $n\to +\infty$ 时，$\dfrac {x^2}4+\dfrac {y^2}{4+\dfrac 1n}=1\to \dfrac {x^2}4+\dfrac {y^2}4=1$．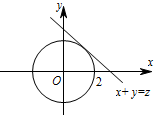
设 $x+y=z$，则当 $x+y=z$ 和圆 $\dfrac {x^2}4+\dfrac {y^2}4=1$ 相切时，$z$ 取最大值．此时 $x+y=2\sqrt 2$，所以 $ \lim \limits_{n \to \infty } {M_n} =2\sqrt 2$．
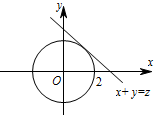设 $x+y=z$，则当 $x+y=z$ 和圆 $\dfrac {x^2}4+\dfrac {y^2}4=1$ 相切时，$z$ 取最大值．此时 $x+y=2\sqrt 2$，所以 $ \lim \limits_{n \to \infty } {M_n} =2\sqrt 2$．
题目
答案
解析
备注
