查看数据源：5912af2ae020e7000a798c0f
在正三棱柱 $ABC-{A_1}{B_1}{C_1}$ 中，若 $AB=\sqrt2B{B_1}$，则 $A{B_1}$ 与 ${C_1}B$ 所成的角的大小是 \((\qquad)\)
A: $60^{\circ}$
B: $75^{\circ}$
C: $90^{\circ}$
D: $105^{\circ}$
【难度】
【出处】
2006年复旦大学自主选拔录取申请资格测试（B卷）
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    异面直线垂直
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    三垂线定理
【答案】
C
【解析】
取 $A_1B_1$ 的中点，记为 $M$，连接 $BM$，如图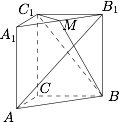：有 $ BM\perp AB_1 $ 且 $ C_1M\perp AB_1 $，于是 $ AB_1\perp BMC_1 $，从而 $ AB_1\perp C_1B$．
题目 答案 解析 备注
0.163957s