如图，已知边长为 $1$ 的正三角形 $A'BC$ 的顶点 $A'$ 在平面 $\alpha$ 内，顶点 $B$、$C$ 在平面 $\alpha$ 外的同一侧，点 $B'$、$C'$ 分别为 $B$、$C$ 在平面 $\alpha$ 内的投影，设 $BB'\leqslant CC'$，直线 $CB'$ 与平面 $A'CC'$ 所成的角为 $\varphi$．若 $\triangle A'B'C'$ 是以角 $A'$ 为直角的直角三角形，则 $\tan\varphi$ 的值可以为 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
BC
【解析】
如图建立空间直角坐标系，设 $B(0,b,m)$，$C(c,0,n)$．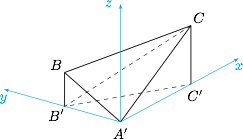
可得$$\begin{cases}b^2+m^2=c^2+n^2=1,\\ (0,b,m)\cdot (c,0,n) =\dfrac 12,\\0<m\leqslant n,\end{cases}$$可得 $m$ 的范围是 $\left(\dfrac{1}{2},\dfrac{\sqrt 2}2\right]$，而$$\tan\varphi =b=\sqrt{1-m^2},$$因此其取值范围为 $\left[\dfrac{\sqrt 2}2,\dfrac{\sqrt 3}2\right)$．
可得$$\begin{cases}b^2+m^2=c^2+n^2=1,\\ (0,b,m)\cdot (c,0,n) =\dfrac 12,\\0<m\leqslant n,\end{cases}$$可得 $m$ 的范围是 $\left(\dfrac{1}{2},\dfrac{\sqrt 2}2\right]$，而$$\tan\varphi =b=\sqrt{1-m^2},$$因此其取值范围为 $\left[\dfrac{\sqrt 2}2,\dfrac{\sqrt 3}2\right)$．
题目
答案
解析
备注
