如果平面 $\alpha,\beta$，直线 $m,n$，点 $A,B$ 满足：$\alpha \parallel \beta$，$m \subset \alpha$，$n \subset \beta$，$A \in m$，$B \in n$，且 $AB$ 与 $\alpha $ 所成的角为 $\dfrac{\pi}{4}$，$n \perp AB$，$m$ 与 $AB$ 所成的角为 $\dfrac{\pi}{3}$．那么 $m$ 与 $n$ 所成角的大小为 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
如图，设 $B$ 在 $\alpha $ 内的射影为 $H$，则 $\angle BAH = \dfrac{\pi}{4}$．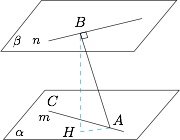
由三射线定理，$$\cos \angle BAH \cdot \cos \angle CAH = \cos \angle BAC,$$所以$$\cos \angle CAH = \dfrac{{\cos \angle BAC}}{{\cos \angle BAH}} = \dfrac{{\sqrt 2 }}{2},$$因此 $\angle CAH = \dfrac{\pi}{4}$．
因为 $n\perp AB$，所以 $n\perp AH$，因此 $m$ 与 $n$ 所成角与 $\angle CAH$ 互余，因此 $m$ 与 $n$ 所成角为 $\dfrac{\pi}{4}$．
由三射线定理，$$\cos \angle BAH \cdot \cos \angle CAH = \cos \angle BAC,$$所以$$\cos \angle CAH = \dfrac{{\cos \angle BAC}}{{\cos \angle BAH}} = \dfrac{{\sqrt 2 }}{2},$$因此 $\angle CAH = \dfrac{\pi}{4}$．因为 $n\perp AB$，所以 $n\perp AH$，因此 $m$ 与 $n$ 所成角与 $\angle CAH$ 互余，因此 $m$ 与 $n$ 所成角为 $\dfrac{\pi}{4}$．
题目
答案
解析
备注
