已知函数 $f\left(x\right)=\begin{cases}\dfrac{1}{x+1}-3,&x\in\left(-1,0\right], \\ x,&x\in\left(0,1\right], \end{cases}$ 且 $g\left(x\right)=f\left(x\right)-mx-m$ 在 $\left(-1,1\right]$ 内有且仅有两个不同的零点，则实数 $m$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2014年高考重庆卷（文）
【标注】
【答案】
A
【解析】
问题即恒过点 $(-1,0)$，且斜率为 $m$ 的直线 $y=m(x+1)$ 与函数 $f(x)$ 的图象有且仅有两个不同的公共点，如图．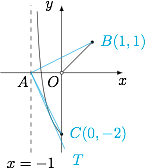
容易计算得直线 $AB$ 的斜率为 $\dfrac 12$，直线 $AC$ 的斜率为 $-2$，设切线 $AT$ 的斜率为 $k$，则联立直线 $y=k(x+1)$ 与双曲线 $y=\dfrac{1}{x+1}-3$ 的方程，得$$k(x+1)^2+3(x+1)-1=0,$$视其为关于 $x+1$ 的二次方程，判别式$$\Delta=9+4k=0,$$解得 $k=-\dfrac 94$．
综上，直线 $y=m(x+1)$ 的斜率 $m$ 的取值范围是 $\left(-\dfrac94,-2\right]\cup \left(0,\dfrac12\right]$．
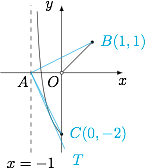容易计算得直线 $AB$ 的斜率为 $\dfrac 12$，直线 $AC$ 的斜率为 $-2$，设切线 $AT$ 的斜率为 $k$，则联立直线 $y=k(x+1)$ 与双曲线 $y=\dfrac{1}{x+1}-3$ 的方程，得$$k(x+1)^2+3(x+1)-1=0,$$视其为关于 $x+1$ 的二次方程，判别式$$\Delta=9+4k=0,$$解得 $k=-\dfrac 94$．综上，直线 $y=m(x+1)$ 的斜率 $m$ 的取值范围是 $\left(-\dfrac94,-2\right]\cup \left(0,\dfrac12\right]$．
题目
答案
解析
备注
