设 $A$ 是以 $BC$ 为直径的圆上的一点，$D,E$ 是线段 $BC$ 上的点，$F$ 是 $CB$ 延长线上的点，已知 $BF=4$，$BD=2$，$BE=5$，$\angle BAD=\angle ACD$，$\angle BAF=\angle CAE$，则 $BC$ 的长为 \((\qquad)\)
【难度】
【出处】
2016年北京大学博雅计划试题
【标注】
【答案】
A
【解析】
如图．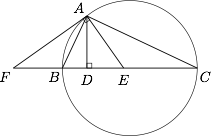
因为 $\angle BAF=\angle CAE$，于是 $AE\perp AF$．
又因为 $\angle BAD=\angle ACD$，于是 $AD\perp BC$．故$$AD^2=DE\cdot DF=DB\cdot DC,$$解得 $DC=9$，从而 $BC=11$．
因为 $\angle BAF=\angle CAE$，于是 $AE\perp AF$．又因为 $\angle BAD=\angle ACD$，于是 $AD\perp BC$．故$$AD^2=DE\cdot DF=DB\cdot DC,$$解得 $DC=9$，从而 $BC=11$．
题目
答案
解析
备注
