两个圆内切于 $K$，大圆的弦 $AB$ 与小圆切于 $L$，已知 $AK:BK=2:5$，$AL=10$，则 $BL$ 的长为 \((\qquad)\)
【难度】
【出处】
2016年北京大学博雅计划试题
【标注】
【答案】
B
【解析】
如图，设 $BK$ 与小圆交于 $M$，连接 $ML$，$CD$ 为两圆在 $K$ 处的公切线．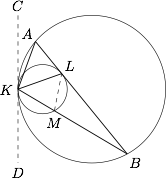
由弦切角定理，得$$\angle DKM=\angle BAK=\angle KLM,$$又 $\angle KLA=\angle KML$，于是可得 $\angle AKL=\angle BKL$，因此由角平分线定理可得 $AL:BL=AK:BK$，从而可得 $BL=25$．
由弦切角定理，得$$\angle DKM=\angle BAK=\angle KLM,$$又 $\angle KLA=\angle KML$，于是可得 $\angle AKL=\angle BKL$，因此由角平分线定理可得 $AL:BL=AK:BK$，从而可得 $BL=25$．
题目
答案
解析
备注
