已知 $a+b+c=1$，则 $\sqrt{4a+1}+\sqrt{4b+1}+\sqrt{4c+1}$ 的最大值与最小值的乘积属于区间 \((\qquad)\)
【难度】
【出处】
2016年北京大学博雅计划试题
【标注】
【答案】
C
【解析】
设函数 $f(x)=\sqrt{4x+1}$ 的图象，则其导函数$$f'(x)=\dfrac{2}{\sqrt{4x+1}}.$$作出函数 $f(x)$ 的图象，函数 $f(x)$ 的图象在 $x=\dfrac 13$ 处的切线$$y=\dfrac{2\sqrt{21}}7\left(x-\dfrac 13\right)+\dfrac{\sqrt{21}}3,$$以及函数 $f(x)$ 的图象过点 $\left(-\dfrac 14,0\right)$ 和 $\left(\dfrac 32,\sqrt 7\right)$ 的割线 $y=\dfrac{4}{\sqrt 7}x+\dfrac{1}{\sqrt 7}$，如图．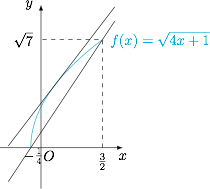
于是可得$$\dfrac{4}{\sqrt 7}x+\dfrac{1}{\sqrt 7}\leqslant \sqrt{4x+1}\leqslant \dfrac{2\sqrt{21}}7\left(x-\dfrac 13\right)+\dfrac{\sqrt{21}}3,$$左侧等号当 $x=-\dfrac 14$ 或 $x=\dfrac 32$ 时取得；右侧等号当 $x=\dfrac 13$ 时取得．因此原式的最大值为 $\sqrt{21}$，当 $a=b=c=\dfrac 13$ 时取得；最小值为 $\sqrt{7}$，当 $a=b=-\dfrac 14$，$c=\dfrac 32$ 时取得．
从而原式最大值与最小值的乘积为 $7\sqrt{3}=\sqrt{147}\in[\sqrt{144},\sqrt{169})$．
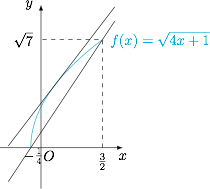于是可得$$\dfrac{4}{\sqrt 7}x+\dfrac{1}{\sqrt 7}\leqslant \sqrt{4x+1}\leqslant \dfrac{2\sqrt{21}}7\left(x-\dfrac 13\right)+\dfrac{\sqrt{21}}3,$$左侧等号当 $x=-\dfrac 14$ 或 $x=\dfrac 32$ 时取得；右侧等号当 $x=\dfrac 13$ 时取得．因此原式的最大值为 $\sqrt{21}$，当 $a=b=c=\dfrac 13$ 时取得；最小值为 $\sqrt{7}$，当 $a=b=-\dfrac 14$，$c=\dfrac 32$ 时取得．从而原式最大值与最小值的乘积为 $7\sqrt{3}=\sqrt{147}\in[\sqrt{144},\sqrt{169})$．
题目
答案
解析
备注
