在圆内接四边形 $ABCD$ 中，$BD=6$，$\angle ABD=\angle CBD=30^\circ$，则四边形 $ABCD$ 的面积等于 \((\qquad)\)
【难度】
【出处】
2016年北京大学博雅计划试题
【标注】
【答案】
B
【解析】
如图，连接 $AC$．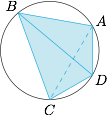
根据题意，有 $CD=AD$ 且 $AC=\sqrt 3AD$，则由托勒密定理可得$$AB\cdot CD+AD\cdot BC=AC\cdot BD,$$即$$AD\cdot (AB+BC)=6\sqrt 3\cdot AD,$$于是 $AB+BC=6\sqrt 3$，进而$$S_{ABCD}=S_{\triangle ABD}+S_{\triangle CBD}=\dfrac 32(AB+BC)=9\sqrt 3.$$
根据题意，有 $CD=AD$ 且 $AC=\sqrt 3AD$，则由托勒密定理可得$$AB\cdot CD+AD\cdot BC=AC\cdot BD,$$即$$AD\cdot (AB+BC)=6\sqrt 3\cdot AD,$$于是 $AB+BC=6\sqrt 3$，进而$$S_{ABCD}=S_{\triangle ABD}+S_{\triangle CBD}=\dfrac 32(AB+BC)=9\sqrt 3.$$
题目
答案
解析
备注
