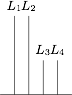
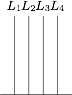
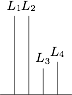
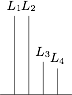
如图，在长方体 $ABCD-{A_1}{B_1}{C_1}{D_1}$ 中，$AB=11$，$AD=7$，$A{A_1}=12$，一质点从顶点 $A$ 射向点 $E\left(4,3,12\right)$，遇长方体的面反射（反射服从光的反射原理）．
将第 $i-1$ 次到第 $i$ 次反射点之间的线段记为 ${L_i}\left(i=2,3,4\right)$，${L_1}=AE$，将线段 ${L_1},{L_2},{L_3},{L_4}$ 竖直放置在同一水平线上，则大致的图形是 \((\qquad)\)
将第 $i-1$ 次到第 $i$ 次反射点之间的线段记为 ${L_i}\left(i=2,3,4\right)$，${L_1}=AE$，将线段 ${L_1},{L_2},{L_3},{L_4}$ 竖直放置在同一水平线上，则大致的图形是 \((\qquad)\)
A:
B:
C:
D:
【难度】
【出处】
2014年高考江西卷（理）
【标注】
【答案】
C
【解析】
将长方体无限拓展出去，如图．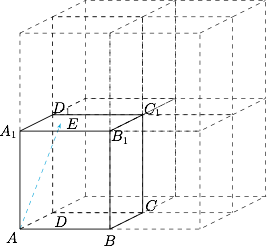
将每个面想象成一个薄膜，让沿 $\overrightarrow{AE}$ 出发的质点沿直线匀速运动并穿透这些薄膜，那么根据反射原理，长方体内的每个反射点都与空间中质点穿透薄膜的位置一一对应（类比于物理中画光的反射光线的方法）．
假设每过 $1$ 单位时间，质点位移均为 $\overrightarrow{AE}=(4,3,12)$．对于左右方向的薄膜，每过 $\dfrac{11}4$ 单位时间均有一个薄膜被穿透；对于前后方面的薄膜，每过 $\dfrac{7}{3}$ 单位时间均有一个薄膜被穿透；对于上下方向的薄膜，每过 $1$ 单位均有一个薄膜被穿透．将这些被穿透的位置按时间序列整理，如图．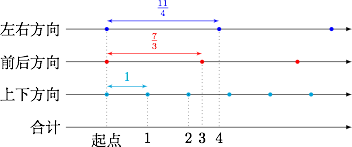
因此 $L_1=L_2=1$，$L_3=\dfrac 73-2=\dfrac 13$，$L_4=\dfrac {11}4-\dfrac 73=\dfrac {5}{12}$（以 $\overrightarrow{AE}$ 的长度为单位）．
将每个面想象成一个薄膜，让沿 $\overrightarrow{AE}$ 出发的质点沿直线匀速运动并穿透这些薄膜，那么根据反射原理，长方体内的每个反射点都与空间中质点穿透薄膜的位置一一对应（类比于物理中画光的反射光线的方法）．假设每过 $1$ 单位时间，质点位移均为 $\overrightarrow{AE}=(4,3,12)$．对于左右方向的薄膜，每过 $\dfrac{11}4$ 单位时间均有一个薄膜被穿透；对于前后方面的薄膜，每过 $\dfrac{7}{3}$ 单位时间均有一个薄膜被穿透；对于上下方向的薄膜，每过 $1$ 单位均有一个薄膜被穿透．将这些被穿透的位置按时间序列整理，如图．
因此 $L_1=L_2=1$，$L_3=\dfrac 73-2=\dfrac 13$，$L_4=\dfrac {11}4-\dfrac 73=\dfrac {5}{12}$（以 $\overrightarrow{AE}$ 的长度为单位）．
题目
答案
解析
备注
