查看数据源：590ac1596cddca00092f6f93
已知菱形 $ABCD$ 的边长为 $2$，$\angle BAD ={120^ \circ}$，点 $E$，$F$ 分别在边 $BC$，$DC$ 上，$BE = \lambda BC$，$DF = \mu DC$，若 $\overrightarrow{AE}\cdot \overrightarrow{AF}= 1$，$\overrightarrow{CE}\cdot \overrightarrow{CF}= - \dfrac{2}{3}$，则 $\lambda + \mu =$  \((\qquad)\)
A: $\dfrac{1}{2}$
B: $\dfrac{2}{3}$
C: $\dfrac{5}{6}$
D: $\dfrac{7}{12}$
【难度】
【出处】
2014年高考天津卷（理）
【标注】
  • 知识点
    >
    向量
    >
    向量的线性表示
    >
    三点共线的向量表达
  • 知识点
    >
    向量
    >
    向量的线性表示
    >
    向量的换底公式
【答案】
C
【解析】
如图，统一起点为 $A$，取基底 $\overrightarrow{AB}$ 和 $\overrightarrow{AD}$，则$$\overrightarrow{AB}\cdot\overrightarrow{AB}=\overrightarrow{AD}\cdot\overrightarrow{AD}=4,\overrightarrow{AB}\cdot\overrightarrow{AD}=2\cdot 2\cdot \cos 120^\circ=-2.$$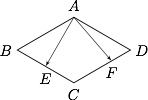向量 $\overrightarrow{AE}=\overrightarrow{AB}+\lambda \overrightarrow{AD}$，$\overrightarrow{AF}=\mu\overrightarrow{AB}+\overrightarrow{AD}$，因此由 $\overrightarrow{AE}\cdot\overrightarrow{AF}=1$ 可得$$\mu\cdot\left(\overrightarrow{AB}\cdot\overrightarrow{AB}\right)+(1+\lambda\mu)\cdot\left(\overrightarrow{AB}\cdot\overrightarrow{AD}\right)+\lambda\cdot\left(\overrightarrow{AD}\cdot\overrightarrow{AD}\right)=1,$$即$$4(\lambda+\mu)-2\lambda\mu=3.$$又由 $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$，从而 $\overrightarrow{CE}=(\lambda-1)\overrightarrow{AD}$，$\overrightarrow{CF}=(\mu-1)\overrightarrow{AB}$，因此由 $\overrightarrow{CE}\cdot\overrightarrow{CF}=-\dfrac 23$ 可得$$\left[\lambda\mu-\left(\lambda+\mu\right)+1\right]\cdot\left(\overrightarrow{AB}\cdot\overrightarrow{AD}\right)=-\dfrac 23,$$即$$\lambda\mu-(\lambda+\mu)=-\dfrac 23.$$由关于 $\lambda$ 和 $\mu$ 的两个方程不难解得 $\lambda+\mu=\dfrac 56$．
题目 答案 解析 备注
0.108544s