查看数据源：590acec96cddca0008610ed4
设复数 $z$ 满足 $2|z|\leqslant |z-1|$，则  \((\qquad)\)
A: $|z|$ 的最大值为 $1$
B: $|z|$ 的最小值为 $\dfrac 13$
C: $z$ 的虚部的最大值为 $\dfrac 23$
D: $z$ 的实部的最大值为 $\dfrac 13$
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
  • 知识点
    >
    复数
    >
    复数的运算
    >
    复数及其运算的几何意义
【答案】
ACD
【解析】
设复平面上 $A(1,0)$，复数 $z$ 对应的点为 $P$，则满足条件的 $P$ 在以 $\left(\dfrac 13,0\right)$，$(-1,0)$ 为直径端点的圆内部（包括圆周），如图．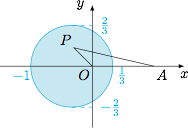
题目 答案 解析 备注
0.112383s