设曲线 $L$ 的方程为 $y^4+\left(2x^2+2\right)y^2+\left(x^4-2x^2\right)=0$,则 \((\qquad)\)
【难度】
【出处】
2015年清华大学自主招生暨领军计划试题
【标注】
【答案】
A
【解析】
记 $f(x,y)=y^4+(2x^2+2)y^2+(x^4-2x^2)$,则
对于选项A、B,由于 $f(-x,y)=f(-x,-y)=f(x,y)$,于是 $L$ 既为轴对称图形,也为中心对称图形;
对于选项C,由于 $y^2=\sqrt{4x^2+1}-(x^2+1)$,令 $y=0$,可得 $x=\pm \sqrt 2,0$,因此选项C错误;
对于选项D,由于 $x^2=-y^2+1\pm\sqrt{-4y^2+1}$,于是 $-4y^2+1\geqslant 0$,即 $-\dfrac 12\leqslant y\leqslant \dfrac 12$.
事实上,该方程对应的曲线如图.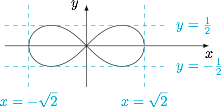
对于选项A、B,由于 $f(-x,y)=f(-x,-y)=f(x,y)$,于是 $L$ 既为轴对称图形,也为中心对称图形;
对于选项C,由于 $y^2=\sqrt{4x^2+1}-(x^2+1)$,令 $y=0$,可得 $x=\pm \sqrt 2,0$,因此选项C错误;
对于选项D,由于 $x^2=-y^2+1\pm\sqrt{-4y^2+1}$,于是 $-4y^2+1\geqslant 0$,即 $-\dfrac 12\leqslant y\leqslant \dfrac 12$.
事实上,该方程对应的曲线如图.
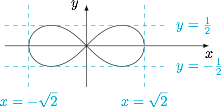
题目
答案
解析
备注