条件 ① 的含义为函数图象的端点是确定的；
条件 ② 的含义为函数图象上任意两点的斜率 $\dfrac{f(x)-f(y)}{x-y}$ 在 $\left(-\dfrac 12,\dfrac 12\right)$ 之间，也就是说函数图象的增长/减少速度是受限的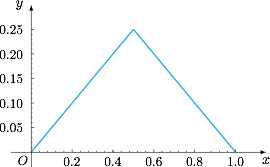；题目要求的 $k$ 的最小值也即为函数 $f(x)$ 的值域长度的最大值，由于函数图象从 $(0,0)$ 出发，最终要回到 $(1,0)$，于是考虑 $f\left(\dfrac 12\right)$．显然在区间 $\left[0,\dfrac 12\right]$ 上，函数值改变量的上界为 $\dfrac 14$．于是函数 $f(x)$ 的值域长度的最大值为 $\dfrac 14$，如图．
下面进行代数描述：
一方面，当 $f(x)$ 的图象无限接近函数$$y=\dfrac 14-\dfrac 12\left|\dfrac 12-x\right|, x\in [0,1]$$的图象时，函数 $f(x)$ 的值域长度无限接近于 $\dfrac 14$；
另一方面，若 $f(x)$ 的值域长度大于或等于 $\dfrac 14$，则必然存在 $m\in (0,1)$ 使得$$\left|f(m)\right|\geqslant \dfrac 14,$$此时若 $m\in\left(0,\dfrac 12\right]$，则令 $x=m$ 且 $y=0$ 即可推出$$\left|f(m)-f(0)\right|<\dfrac 12\left|m-0\right|,$$矛盾．
类似的，当 $m\in\left(\dfrac 12,1\right)$，可以令 $x=m$ 且 $y=1$ 推出矛盾．
因此所求的 $k$ 的最小值为 $\dfrac 14$．