设双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\left(a>0,b>0\right)$ 的右焦点为 $F$，右顶点为 $A$，过 $F$ 作 $AF$ 的垂线与双曲线交于 $B,C$ 两点，过 $B,C$ 分别作 $AC,AB$ 的垂线，两垂线交于点 $D$．若 $D$ 到直线 $BC$ 的距离小于 $a+\sqrt{a^2+b^2}$，则该双曲线的渐近线斜率的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
过双曲线的焦点且垂直于实轴的弦称为双曲线的通径，其长度为 $2\cdot\dfrac{b^2}{a}$．
根据题意有 $A(a,0)$，$B\left(c,\dfrac{b^2}{a}\right)$，$C\left(c,-\dfrac{b^2}a\right)$，$D(m,0)$．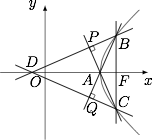
由 $CA\perp BD$ 可得 $\overrightarrow {AC}\cdot\overrightarrow {DB}=0$，从而$$\left(c-a,-\dfrac{b^2}a\right)\cdot\left(c-m,\dfrac{b^2}{a}\right)=0,$$即$$(c-a)(c-m)=\dfrac{b^4}{a^2}.$$题目要求 $D$ 到直线 $BC$ 的距离小于 $a+\sqrt{a^2+b^2}$，即 $m>-a$，因此$$\dfrac{b^4}{a^2}=(c-a)(c-m)<(c-a)(c+a)=b^2,$$进而 $\dfrac{b^2}{a^2}<1$，于是双曲线的渐近线斜率的取值范围是 $(-1,0)\cup(0,1)$．
根据题意有 $A(a,0)$，$B\left(c,\dfrac{b^2}{a}\right)$，$C\left(c,-\dfrac{b^2}a\right)$，$D(m,0)$．
由 $CA\perp BD$ 可得 $\overrightarrow {AC}\cdot\overrightarrow {DB}=0$，从而$$\left(c-a,-\dfrac{b^2}a\right)\cdot\left(c-m,\dfrac{b^2}{a}\right)=0,$$即$$(c-a)(c-m)=\dfrac{b^4}{a^2}.$$题目要求 $D$ 到直线 $BC$ 的距离小于 $a+\sqrt{a^2+b^2}$，即 $m>-a$，因此$$\dfrac{b^4}{a^2}=(c-a)(c-m)<(c-a)(c+a)=b^2,$$进而 $\dfrac{b^2}{a^2}<1$，于是双曲线的渐近线斜率的取值范围是 $(-1,0)\cup(0,1)$．
题目
答案
解析
备注
