若不等式组 $\begin{cases}x+y-2\leqslant 0,\\ x+2y-2\geqslant 0,\\ x-y+2m\geqslant 0\end{cases}$ 表示的平面区域为三角形，且其面积等于 $\dfrac 43$，则 $m$ 的值为 \((\qquad)\)
【难度】
【出处】
2015年高考重庆卷（文）
【标注】
【答案】
B
【解析】
如图，画出不等式组表示的平面区域，直线 $x+y-2=0$ 和直线 $x+2y-2=0$ 均交 $x$ 轴于 $A(2,0)$，直线 $x-y+2m=0$ 与直线 $x+y-2=0$、直线 $x+2y-2=0$ 和 $x$ 轴分别交于点 $P$、$Q$ 和 $B$．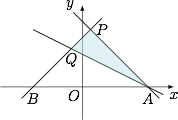
根据题意，当 $B$ 点位于 $A$ 点左侧，即 $-2m<2$ 时，不等式组表示三角形区域（$\triangle APQ$ 的边界以及内部），此时区域面积为$$S_{\triangle APQ}=S_{\triangle PBA}-S_{\triangle QBA}=\dfrac 12\cdot (x_A-x_B)\cdot (y_P-y_Q),$$经计算可得$$x_B=-2m,y_P=m+1,y_Q=\dfrac 23(m+1),$$因此$$S_{\triangle APQ}=\dfrac 12\cdot (2+2m)\cdot \dfrac 13(m+1)=\dfrac 43,$$解得 $m=-3$（舍去），或 $m=1$．
根据题意，当 $B$ 点位于 $A$ 点左侧，即 $-2m<2$ 时，不等式组表示三角形区域（$\triangle APQ$ 的边界以及内部），此时区域面积为$$S_{\triangle APQ}=S_{\triangle PBA}-S_{\triangle QBA}=\dfrac 12\cdot (x_A-x_B)\cdot (y_P-y_Q),$$经计算可得$$x_B=-2m,y_P=m+1,y_Q=\dfrac 23(m+1),$$因此$$S_{\triangle APQ}=\dfrac 12\cdot (2+2m)\cdot \dfrac 13(m+1)=\dfrac 43,$$解得 $m=-3$（舍去），或 $m=1$．
题目
答案
解析
备注
