在平面内，定点 $A,B,C,D$ 满足 $\big|\overrightarrow{DA}\big|=\big|\overrightarrow{DB}\big|=\big|\overrightarrow{DC}\big|$，$\overrightarrow{DA}\cdot\overrightarrow{DB}=\overrightarrow{DB}\cdot\overrightarrow{DC}=\overrightarrow{DC}\cdot\overrightarrow{DA}=-2$，动点 $P,M$ 满足 $\big|\overrightarrow{AP}\big|=1$，$\overrightarrow{PM}=\overrightarrow{MC}$，则 $\big|\overrightarrow{BM}\big|^2$ 的最大值是 \((\qquad)\)
【难度】
【出处】
2016年高考四川卷（理）
【标注】
【答案】
B
【解析】
根据已知，有 $\angle ADB=\angle BDC=\angle CDA$，因此 $\triangle DAB,\triangle DBC,\triangle DCA$ 全等，进而可得 $\triangle ABC$ 为正三角形，进一步计算可得 $DA=DB=DC=2$．
根据题意，$P$ 在以 $A$ 为圆心 $1$ 为半径的圆上运动，因此 $CP$ 的中点 $M$ 在以 $N$ 为圆心，$\dfrac 12$ 为半径的圆上运动，其中 $N$ 点为边 $AC$ 的中点，如图．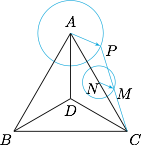
因此 $\big|\overrightarrow{BM}\big|^2$ 的最大值为$$\left(BN+\dfrac 12\right)^2=\left(\dfrac 32DB+\dfrac 12\right)^2=\dfrac{49}4,$$选B．
根据题意，$P$ 在以 $A$ 为圆心 $1$ 为半径的圆上运动，因此 $CP$ 的中点 $M$ 在以 $N$ 为圆心，$\dfrac 12$ 为半径的圆上运动，其中 $N$ 点为边 $AC$ 的中点，如图．
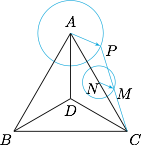因此 $\big|\overrightarrow{BM}\big|^2$ 的最大值为$$\left(BN+\dfrac 12\right)^2=\left(\dfrac 32DB+\dfrac 12\right)^2=\dfrac{49}4,$$选B．
题目
答案
解析
备注
