设直线 $l_1,l_2$ 分别是函数 $f(x)=\begin{cases} -\ln x,&0<x<1,\\ \ln x,&x>1\end{cases}$ 图象上点 $P_1,P_2$ 处的切线，$l_1$ 与 $l_2$ 垂直相交于点 $P$，且 $l_1,l_2$ 分别与 $y$ 轴相交于点 $A,B$，则 $\triangle PAB$ 的面积的取值范围是 \((\qquad)\)
【难度】
【出处】
2016年高考四川卷（文）
【标注】
【答案】
A
【解析】
由于 $(-\ln x)'=-\dfrac 1x<0$，而 $(\ln x)'=\dfrac 1x>0$，于是若两条切线互相垂直，则切点必然分别位于图象在 $(0,1)$ 和 $(1,+\infty)$ 的部分，如图．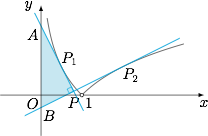
设 $P_1(t,-\ln t)$（$0<t<1$），则不难计算得 $P_2\left(\dfrac 1t,-\ln t\right)$，两条切线分别为$$l_1:y=-\dfrac 1tx+1-\ln t,l_2:y=tx-1-\ln t,$$进而可得 $\triangle PAB$ 的面积$$S=\dfrac 12\cdot x_P\cdot |AB|=\dfrac{2}{t+\dfrac 1t},$$其取值范围是 $(0,1)$，选A．
设 $P_1(t,-\ln t)$（$0<t<1$），则不难计算得 $P_2\left(\dfrac 1t,-\ln t\right)$，两条切线分别为$$l_1:y=-\dfrac 1tx+1-\ln t,l_2:y=tx-1-\ln t,$$进而可得 $\triangle PAB$ 的面积$$S=\dfrac 12\cdot x_P\cdot |AB|=\dfrac{2}{t+\dfrac 1t},$$其取值范围是 $(0,1)$，选A．
题目
答案
解析
备注
