函数 $f\left( x \right) = 1 - \left| {1 - 2x} \right|, x \in \left[ {0, 1} \right]$，$g\left( x \right) = {x^2} - 2x + 1, x \in \left[ {0, 1} \right]$，定义函数 $F\left( x \right) =\begin{cases}
f\left( x \right), &f\left( x \right) \geqslant g\left( x \right) ,\\
g\left( x \right),& f\left( x \right) < g\left( x \right),\\
\end{cases}$ 那么方程 $F\left( x \right) \cdot {2^x} = 1$ 的实数解的个数是 \((\qquad)\)
f\left( x \right), &f\left( x \right) \geqslant g\left( x \right) ,\\
g\left( x \right),& f\left( x \right) < g\left( x \right),\\
\end{cases}$ 那么方程 $F\left( x \right) \cdot {2^x} = 1$ 的实数解的个数是 \((\qquad)\)
【难度】
【出处】
2008年上海财经大学自主招生试题
【标注】
【答案】
D
【解析】
设 $h(x)=2^{-x}$，如图．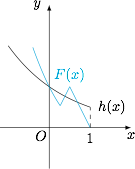
在 $[0,1]$ 上共有 $3$ 个实数解．
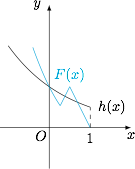在 $[0,1]$ 上共有 $3$ 个实数解．
题目
答案
解析
备注
