查看数据源：5a3df570fab70800079178c5
已知 $O$ 为 $\triangle ABC$ 的外心，$\angle ABC=60^\circ$，$\overrightarrow{BO}=\lambda\overrightarrow{BA}+\mu\overrightarrow{BC}$，则 \((\qquad)\)
A: $\lambda+\mu$ 的最小值为 $\dfrac 12$，此时 $\triangle ABC$ 为直角三角形
B: $\lambda+\mu$ 的最大值为 $\dfrac 12$，此时 $\triangle ABC$ 为直角三角形
C: $\lambda+\mu$ 的最小值为 $\dfrac 23$，此时 $\triangle ABC$ 为等边三角形
D: $\lambda+\mu$ 的最大值为 $\dfrac 23$，此时 $\triangle ABC$ 为等边三角形
【难度】
【出处】
2017年清华大学THUSSAT附加学科测试数学部分（二测）
【标注】
  • 数学竞赛
    >
    平面向量
    >
    平面向量
  • 知识点
    >
    向量
    >
    向量的线性表示
    >
    等系数和线
【答案】
D
【解析】
如图．延长 $BO$ 交直线 $AC$ 于 $D$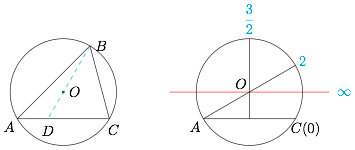．根据向量线性分解的系数和线，可得\[\overrightarrow{BO}=(\lambda+\mu)\overrightarrow{BD},\]记 $\overrightarrow{BO}$ 的数量为 $1$，则 $\overrightarrow{BD}$ 的数量取值范围是 $(-\infty,0)\cup\left[\dfrac 32,+\infty\right)$，于是 $\lambda+\mu$ 的取值范围是 $\left(-\infty,\dfrac 23\right]$．当 $\triangle ABC$ 为等边三角形时，$\lambda+\mu$ 取得最大值为 $\dfrac 23$；当 $\triangle ABC$ 为直角三角形时，$\lambda+\mu=\dfrac 12$．
题目 答案 解析 备注
0.204246s