查看数据源：5a3e2380fab7080008a76a7b
把不超过实数 $x$ 最大整数记为 $[x]$，任取互质且不小于 $3$ 的正奇数 $m,n$，令\[I=\sum_{i=1}^{\frac{m-1}2}\left[\dfrac{ni}{m}\right]+\sum_{j=1}^{\frac{n-1}2}\left[\dfrac{mi}{n}\right],\]则 \((\qquad)\)
A: $I<\dfrac{m-1}2\cdot \dfrac{n-1}2$
B: $I>\dfrac{m-1}2\cdot \dfrac{n-1}2$
C: $I\leqslant\dfrac{m-1}2\cdot \dfrac{n-1}2$
D: $I\geqslant\dfrac{m-1}2\cdot \dfrac{n-1}2$
【难度】
【出处】
2017年清华大学THUSSAT附加学科测试数学部分（二测）
【标注】
  • 数学竞赛
    >
    简单组合
    >
    简单组合
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    高斯函数
  • 方法
    >
    思考方式
    >
    算两次
  • 方法
    >
    数形结合
    >
    构造几何图形
【答案】
CD
【解析】
如图，构造 $m\times n$ 的一个网格，$OP$ 为其对角线，则题中和式的两部分分别为 $\dfrac {m}2\times \dfrac{n}2$ 的矩形内部在对角线 $OP$ 上、下部分的格点数（由于 $m,n$ 互质，于是对角线上没有 $(0,0)$ 和 $(m,n)$ 以外的格点），因此\[I=\dfrac{m-1}2\cdot \dfrac{n-1}2.\]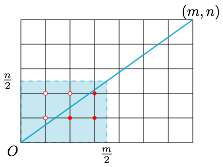
题目 答案 解析 备注
0.157948s