对于具有相同定义域 $D$ 的函数 $f\left(x\right)$ 和 $g\left(x\right)$，若存在函数 $h\left(x\right) = kx + b$（$k,b$ 为常数），对任给的正数 $m$，存在相应的 ${x_0} \in D$，使得当 $x \in D$ 且 $x > {x_0}$ 时，总有 $ {\begin{cases}
0 < f\left(x\right) - h\left(x\right) < m, \\
0 < h\left(x\right) - g\left(x\right) < m, \\
\end{cases}} $ 则称直线 $l:y = kx + b$ 为曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 的 " 分渐近线 "．给出定义域均为 $D= \left\{ {x\left| \right.{x > 1} } \right\}$ 的四组函数如下：
① $f\left(x\right) = {x^2}$，$g\left(x\right) = \sqrt x $；
② $f\left(x\right) = {10^{ - x}} + 2$，$g\left(x\right) = $ $\dfrac{2x - 3}{x}$；
③ $f\left(x\right)=\dfrac{{{x^2} + 1}}{x}$，$g\left(x\right) = $ $\dfrac{x\ln x + 1}{\ln x}$；
④ $f\left(x\right) = \dfrac{{2{x^2}}}{x + 1}$，$g\left(x\right) = 2\left(x - 1 - { {\mathrm{e }} ^{ - x}}\right)$．
其中，曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 存在 " 分渐近线 " 的是 \((\qquad)\)
0 < f\left(x\right) - h\left(x\right) < m, \\
0 < h\left(x\right) - g\left(x\right) < m, \\
\end{cases}} $ 则称直线 $l:y = kx + b$ 为曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 的 " 分渐近线 "．给出定义域均为 $D= \left\{ {x\left| \right.{x > 1} } \right\}$ 的四组函数如下：
① $f\left(x\right) = {x^2}$，$g\left(x\right) = \sqrt x $；
② $f\left(x\right) = {10^{ - x}} + 2$，$g\left(x\right) = $ $\dfrac{2x - 3}{x}$；
③ $f\left(x\right)=\dfrac{{{x^2} + 1}}{x}$，$g\left(x\right) = $ $\dfrac{x\ln x + 1}{\ln x}$；
④ $f\left(x\right) = \dfrac{{2{x^2}}}{x + 1}$，$g\left(x\right) = 2\left(x - 1 - { {\mathrm{e }} ^{ - x}}\right)$．
其中，曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 存在 " 分渐近线 " 的是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
根据题意，可以知道\[\lim_{x\to +\infty}{\dfrac {f\left(x\right)}{x}} = \lim_{x\to+ \infty}{\dfrac {g\left(x\right)}{x}}= k, \]以及在此基础上\[\lim_{x\to +\infty}\left({f\left(x\right)-kx}\right) = \lim_{x\to+ \infty}\left({g\left(x\right)-kx}\right)= b \]是 $f\left(x\right)$ 与 $g\left(x\right)$ 存在“分渐近线”的必要条件．由第一个条件可以排除 $ ① $；由第二个条件可以排除 $ ③ $．事实上，可以计算出对于 $ ② $，“分渐近线”的方程为 $ y= 2 $，如图：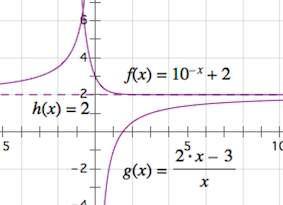
对于 $ ④ $，“分渐近线”的方程为 $ y= 2x -2$，如图：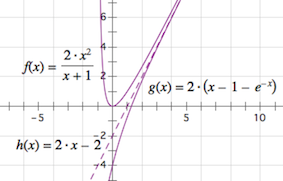
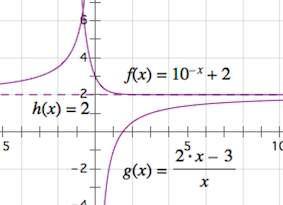对于 $ ④ $，“分渐近线”的方程为 $ y= 2x -2$，如图：
题目
答案
解析
备注
