已知四面体 $ABCD$ 内接于球 $O$，且 $AD$ 是球 $O$ 的直径．若 $\triangle ABC$ 和 $\triangle BCD$ 都是边长为 $1$ 的等边三角形，则四面体 $ABCD$ 的体积是 \((\qquad)\) ．
【难度】
【出处】
2018年全国高中数学联赛陕西省预赛（第一试）
【标注】
【答案】
B
【解析】
如图，设 $O_1$ 为等边 $\triangle ABC$ 的中心，所以 $OO_1\bot$ 平面 $ABC$，$O_1A=\dfrac{\sqrt{3}}{2}\times\dfrac{2}{3}=\dfrac{\sqrt{3}}{3}$．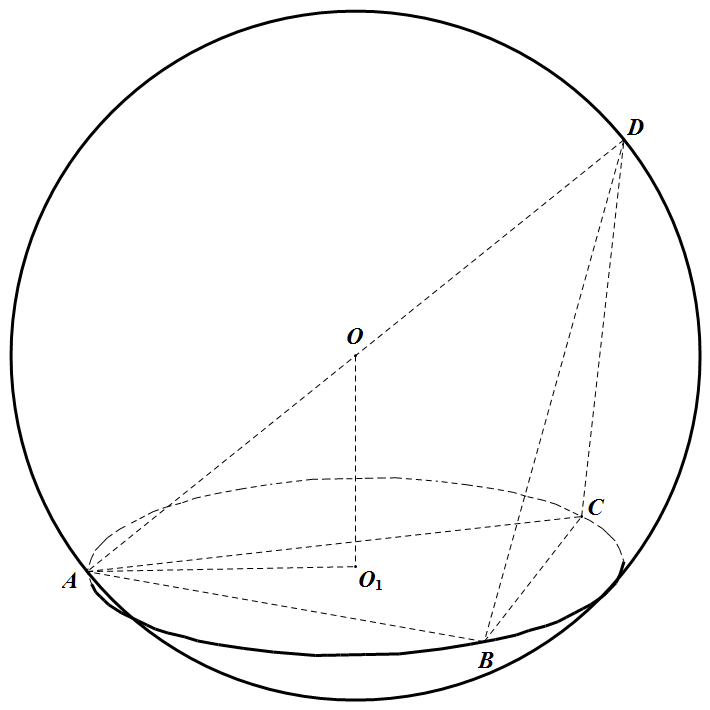
由 $AD$ 是球 $O$ 的直径知，$\angle ABD=90^\circ$．又 $AB=BD=1$，所以 $AD=\sqrt{2}$．在 $Rt\triangle AO_1O$ 中，$O_1O=\sqrt{(\dfrac{AD}{2})^2-O_1A^2}=\dfrac{\sqrt{6}}{6}$．从而，点 $D$ 到平面 $ABC$ 的距离 $d=2OO_1=\dfrac{\sqrt{6}}{6}$．故四面体 $ABCD$ 的体积 $V=\dfrac{1}{3}S_{\triangle ABC}\cdot d=\dfrac{1}{3}\times\dfrac{\sqrt{3}}{4}\times\dfrac{\sqrt{6}}{3}=\dfrac{\sqrt{2}}{12}$．
由 $AD$ 是球 $O$ 的直径知，$\angle ABD=90^\circ$．又 $AB=BD=1$，所以 $AD=\sqrt{2}$．在 $Rt\triangle AO_1O$ 中，$O_1O=\sqrt{(\dfrac{AD}{2})^2-O_1A^2}=\dfrac{\sqrt{6}}{6}$．从而，点 $D$ 到平面 $ABC$ 的距离 $d=2OO_1=\dfrac{\sqrt{6}}{6}$．故四面体 $ABCD$ 的体积 $V=\dfrac{1}{3}S_{\triangle ABC}\cdot d=\dfrac{1}{3}\times\dfrac{\sqrt{3}}{4}\times\dfrac{\sqrt{6}}{3}=\dfrac{\sqrt{2}}{12}$．
题目
答案
解析
备注
