设有三角形 $A_0B_0C_0$，做它的内切圆，三个切点确定一个新的三角形 $A_1B_1C_1$，再做三角形 $A_1B_1C_1$ 的内切圆，三个切点确定三角形 $A_2B_2C_2$，以此类推，一次一次不停地做下去可以得到一个三角形序列，它们的尺寸越来越小，则最终这些三角形的极限情形是 \((\qquad)\)
【难度】
【出处】
2015年北京大学生命科学冬令营试卷数学部分
【标注】
【答案】
A
【解析】
内切圆的顶点的对应关系如下图，为了方便，我们直接用 $A_n,B_n,C_n$ 记 $\triangle A_nB_nC_n$ 的三个内角（$n\in\mathbb{N}$）：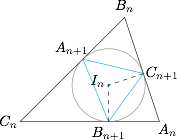
则三角形 $A_nB_nC_n$ 的内切圆圆心 $I_n$ 为三角形 $A_{n+1}B_{n+1}C_{n+1}$ 的外接圆圆心，于是有$$A_{n+1}=\dfrac 12\angle B_{n+1}I_nC_{n+1}=\dfrac 12(\pi-A_n).$$于是有$$A_{n+1}-\dfrac {\pi}{3}=-\dfrac 12\left(A_n-\dfrac{\pi}{3}\right).$$于是有$$A_n=\left(A_0-\dfrac{\pi}{3}\right)\cdot\left(-\dfrac 12\right)^n+\dfrac{\pi}{3},n\in\mathbb{N}.$$所以当 $n\to+\infty$ 时，有 $A_n\to \dfrac{\pi}{3}$，同理有 $n\to +\infty, B_n\to\dfrac{\pi}{3}, C_n\to\dfrac{\pi}{3}$，所以 $\triangle A_nB_nC_n$ 的极限情形为等边三角形．
也可以直接由 $2A_{n+1}+A_n=\pi$，得到 $A_{n+1}=\dfrac {B_n+C_n}{2}$，从而得到这些三角形的极限情况是三个内角都相等．
则三角形 $A_nB_nC_n$ 的内切圆圆心 $I_n$ 为三角形 $A_{n+1}B_{n+1}C_{n+1}$ 的外接圆圆心，于是有$$A_{n+1}=\dfrac 12\angle B_{n+1}I_nC_{n+1}=\dfrac 12(\pi-A_n).$$于是有$$A_{n+1}-\dfrac {\pi}{3}=-\dfrac 12\left(A_n-\dfrac{\pi}{3}\right).$$于是有$$A_n=\left(A_0-\dfrac{\pi}{3}\right)\cdot\left(-\dfrac 12\right)^n+\dfrac{\pi}{3},n\in\mathbb{N}.$$所以当 $n\to+\infty$ 时，有 $A_n\to \dfrac{\pi}{3}$，同理有 $n\to +\infty, B_n\to\dfrac{\pi}{3}, C_n\to\dfrac{\pi}{3}$，所以 $\triangle A_nB_nC_n$ 的极限情形为等边三角形．也可以直接由 $2A_{n+1}+A_n=\pi$，得到 $A_{n+1}=\dfrac {B_n+C_n}{2}$，从而得到这些三角形的极限情况是三个内角都相等．
题目
答案
解析
备注
