已知函数 $f(x)={\log_4}x-\left(\dfrac 14\right)^x$ 和函数 $g(x)={\log_{\frac 14}}x-\left(\dfrac 14\right)^x$ 的零点分别为 $x_1,x_2$，则 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
分别作函数 $y={\log_4}x$、$y={\log_{\frac 14}}x$ 与 $y=\left(\dfrac 14\right)^x$ 的图象，得到 $0<x_2<1<x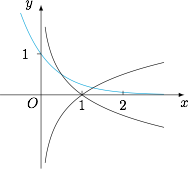_1$．
又因为$${\log_4}x_1-{\log_{\frac 14}}x_2={\log_4}\left(x_1x_2\right)=\left(\dfrac 14\right)^{x_1}-\left(\dfrac 14\right)^{x_2}<0,$$所以 $x_1x_2<1$．
又因为$${\log_4}x_1-{\log_{\frac 14}}x_2={\log_4}\left(x_1x_2\right)=\left(\dfrac 14\right)^{x_1}-\left(\dfrac 14\right)^{x_2}<0,$$所以 $x_1x_2<1$．
题目
答案
解析
备注
